遞迴的第二個練習題是計算最大公因數!
不過除了講遞迴的寫法，還會多寫另外兩種寫法
今天會用到歐幾里得算法，先給大家補充一下!

歐幾里得算法(Euclidean Algorithm)是一種古老而高效的算法，用於計算兩個整數的最大公因數(Greatest Common Divisor,GCD)

歐幾里得算法定理： 兩個數字 a 和 b 的最大公因數等於b和a除以b的餘數的最大公因數
也就是說，gcd(a,b)=gcd(b,a%b)
接下來直接看題目吧~

計算最大公因數

1.遞迴方法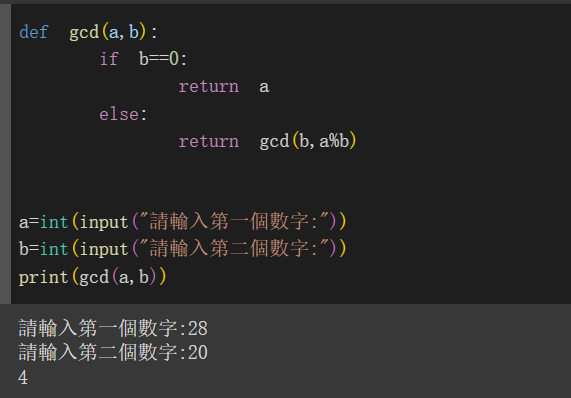

定義一個叫做gcd的函式，它的參數a和b是使用者輸入了兩個數字，利用函式中程式碼去找這兩個數的最大公因數
if b==0這部分就是基本情況，表示遞迴的結束條件!也因為b是0，所以最大公因數就會是a
else的部分就是遞迴情況，也就是當b不等於0這個條件符合的時候執行
return gcd(b, a%b)它呼叫了自己!呼叫gcd去計算gcd(b,a%b)
意思是用 b 和 a除以b 的餘數來替代原來的a和b
這個是根據歐幾里得算法進行的!

再來下面就是輸入部分
最後一行就是輸出gcd(a,b)
看執行結果，我輸入28和20，去跑gcd函式，找到最大公因數是4!

2.內建函式方法

這個方法是要引入模組! import math
這個程式碼更短了~
我隨便輸入50和18，找出最大公因數是2

3.迭代方法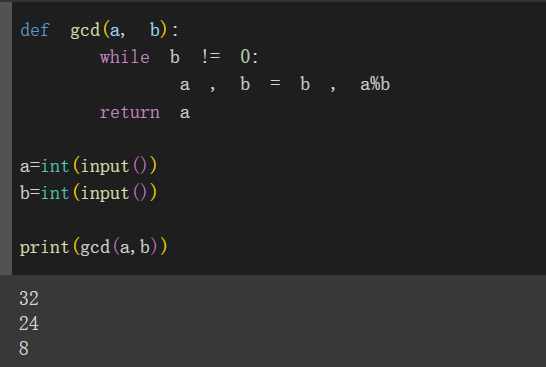

其實程式碼也減少很多~前面一樣先定義gcd函式
迴圈的條件是當b!=0的時候，迴圈才會繼續執行
迴圈裡面執行的程式碼來解釋一下><
a, b = b, a % b這句同時更新了變數的值
a會更新成b的值，而b會更新成a%b的值
這一步的目的是按照歐幾里得算法的定義來更新a和b，將問題轉化為較小的子問題
每次迴圈執行，a和b的值都會變得更小，直到b=0
當b=0的時候，就return a，a就是最大公因數!

後面我輸入32和24
說明一下計算步驟~這樣比較能看懂!

第一次迴圈：
a = 32
b = 24
計算 32 % 24 = 8
更新為 a = 24，b = 8

第二次迴圈：
a = 24
b = 8
計算 24 % 8 = 0
更新為 a = 8，b = 0

結束：
現在b=0，結束迴圈
回傳a的值，也就是8

整理了三種方法的好處或壞處!

1.遞迴方法:它是一種直觀而且也簡單的實現方式，但可能會有額外的遞迴調用開銷
2.內建函數方法:是最簡單、推薦的方法，因為它利用了Python標準函式庫中的高效實現!
3.迭代方法:是一種避免遞迴開銷的實現方式，適合需要高效性能的場合

明天還有最後一題!
我覺得難度比較高一些，跟字串還有排列有關!